アンモニア反応器は、反応器の例題として取り上げられることが多く、例えばDYNSIMでもApplibフォルダ中にいくつかのモデリング例が取り上げられていますが、先日面白い論文を見つけたのでご紹介します。
こちらのBernieさんの論文ですが、公開されている論文の情報をベースにアンモニア反応器の非定常解析を行われています。
アンモニアの合成反応としては、Temkin-Pyzhevの反応式(1940)にAnnableの反応定数(1952)を用いた組み合わせが広く使われています。しかし、上記の組み合わせでは反応定数に圧力項がなく、以下の論文では正反応に対して、圧力の影響も考慮した反応定数(以下のGillespie–Beattie correlation)が紹介されています。
$$ K_p^{GB} = K_p^{GB*} 10^{\alpha – p^*}$$
ここで、αが圧力補正項となっており、以下の式で表されます。( \(K_p^{GB*}\)は温度のみの関数になっています 。なお、温度、圧力の単位系はそれぞれK、atmです。)
$$ \alpha = \frac{0.1191849}{T} + \frac{91.87212}{T^2} + \frac{25122730}{T^4}$$
$$ log (K_p^{GB*}) = -2.69112 log(T) – 5.51926 * 10^{-5} T + 1.84886 * 10 ^ {-7} T^2 + 2001.6 / T_r + 2.6899 $$
参考論文1. Dynamic Model of an Ammonia Synthesis Reactor Based on Open Infomration, Bernt Lie
参考論文2. STABILITY MAP FOR AMMONIA SYNTHESIS REACTORS, Volker Siepmann
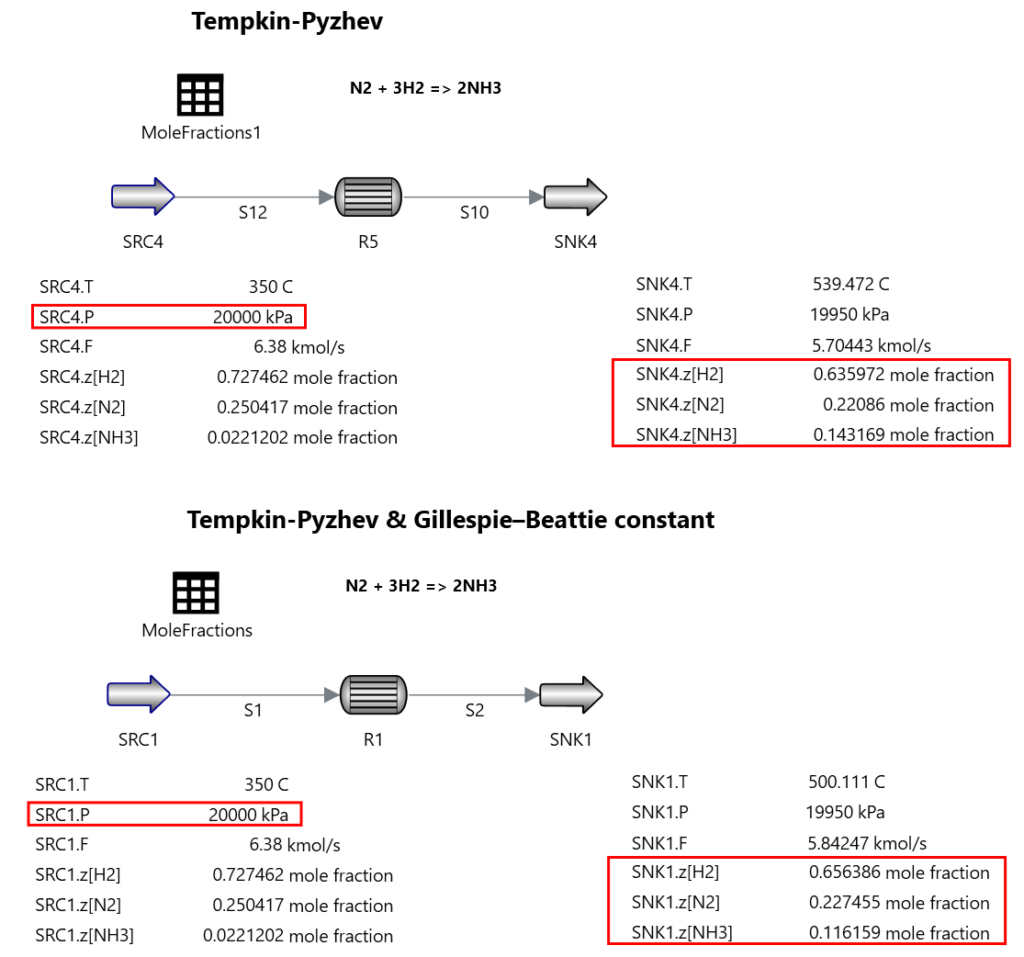
ちょっと反応モデルがややこしいので、AVEVA社のSimCentralで通常のTemkin-Pyzhevの反応式とどの程度の差異が生じるのか比較してみました。(こちらに記載しておりますが、SimCentralの場合は、全ての式がオープンになっており、自由にカスタマイズできるため、このような若干厄介な式もそのまま書けます)
以下が同様の断熱反応で計算させた結果ですが、Gillespie-Beattie equilibrium constantを使うと、圧力補正項の分、反応速度が落ちるようです。


コメント